pengertian logaritma dan sifat-sifatnya
Pengertian Logaritma
Logaritma adalah suatu operasi invers atau kebalikan dari perpangkatan.
Jika diketahui suatu perpangkatan
maka bentuk tersebut dapat dituliskan dalam bentuk logaritma menjadi
dengan a > 0 dan a ≠ 1.
Keterangan:
a = basis logaritma
b = bilangan yang dicari nilai logaritmanya (numerus)
c = besar pangkat / nilai logaritma
Sebagai contoh, misalkan diberikan ²log 8 = c maka c = 3, karena 2³ = 8.
Sehingga dapat disimpulkan bahwa logaritma merupakan suatu operasi kebalikan dari perpangkatan, yaitu mencari nilai yang menjadi pangkat dari suatu bilangan.
Biar lebih paham lagi, perhatikan beberapa contoh dibawah ini.
| Bentuk Perpangkatan | Bentuk Logaritma |
|---|---|
| ³log 81 = 4 | |
| ³log | |
Jika nilai a = 10, biasanya 10 tidak dituliskan sehingga menjadi log b = c.
Sebagai contoh, jika 10³ = 1000 maka dalam bentuk logaritma menjadi log 1000 = 3
Selain itu, logaritma memiliki sifat-sifat yang wajib kita pahami. Karena untuk menyelesaikan soal-soal logaritma kita membutuhkan pemahaman sifat-sifat logaritma tersebut. Apa saja sifat-sifat logaritma? Yuk, perhatikan gambar berikut.
Sifat-sifat Logaritma
1. Sifat Logaritma dari perkalian
Suatu logaritma merupakan hasil penjumlahan dari dua logaritma lain yang nilai kedua numerus-nya merupakan faktor dari nilai numerus awal. Berikut modelnya:
alog p.q = alog p + alog q
dengan syarat a > 0, , p > 0, q > 0.
2. Perkalian Logaritma
Suatu logaritma a dapat dikalikan dengan logaritma b jika nilai numerus logaritma a sama dengan nilai bilangan pokok logaritma b. Hasil perkalian tersebut merupakan logaritma baru dengan nilai bilangan pokok sama dengan logaritma a, dan nilai numerus sama dengan logaritma b. Berikut model sifat logaritma nya:
alog b x blog c = alog c
dengan syarat a > 0, .
3. Sifat Logaritma dari pembagian
Suatu logaritma merupakan hasil pengurangan dari dua logaritma lain yang nilai kedua numerus-nya merupakan pecahan atau pembagian dari nilai numerus logaritma awal. Berikut modelnya:
alog = alog p – alog q
dengan syarat a > 0, , p > 0, q > 0.
4. Sifat Logaritma berbanding terbalik
Suatu logaritma berbanding terbalik dengan logaritma lain yang memiliki nilai bilangan pokok dan numerus-nya saling bertukaran. Berikut modelnya:
alog b =
dengan syarat a > 0, .
5. Logaritma berlawanan tanda
Suatu logaritma berlawanan tanda dengan logaritma yang memiliki numerus-nya merupakan pecahan terbalik dari nilai numerus logaritma awal. Berikut modelnya:
alog = – alog
6. Sifat Logaritma dari perpangkatan
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pengali. Berikut modelnya :
alog bp = p. alog b
dengan syarat a > 0, , b > 0
7. Perpangkatan Bilangan Pokok Logaritma
Suatu logaritma dengan nilai bilangan pokoknya merupakan suatu eksponen (pangkat) dapat dijadikan logaritma baru dengan mengeluarkan pangkatnya menjadi bilangan pembagi. Berikut modelnya:
dengan syarat a > 0, .
8. Bilangan pokok logaritma sebanding dengan perpangkatan numerus
Suatu logaritma dengan nilai numerus-nya merupakan suatu eksponen (pangkat) dari nilai bilangan pokoknya memiliki hasil yang sama dengan nilai pangkat numerus tersebut. Berikut model sifat logaritma nya:
alog ap = p
dengan syarat a > 0 dan .
9. Perpangkatan logaritma
Suatu bilangan yang memiliki pangkat berbentuk logaritma, hasil pangkatnya adalah nilai numerus dari logaritma tersebut. Berikut modelnya:
dengan syarat a > 0, , m > 0.
10. Mengubah basis logaritma
Suatu logaritma dapat dipecah menjadi perbandingan dua logaritma sebagai berikut:
dengan syarat a > 0, , p > 0, q > 0
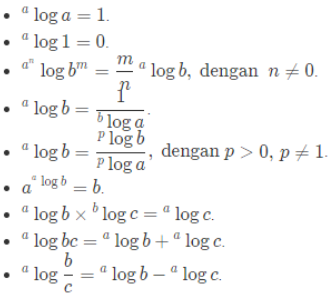
Komentar
Posting Komentar